计算耗尽区

如上一页所述，我们需要做出某些假设才能求二极管方程的解析解。

假设如下：

1. 耗尽区近似：电场仅限于结区，准中性区没有电场。
2. 耗尽区中没有自由载流子 (n(x), p(x) = 0 ) 。
3. 我们可以假设没有自由载流子，因为电场很快将它们扫出耗尽区。没有自由载流子意味着（1）传输方程消失并且（2）没有复合或生成，因此连续性方程变为
   $\frac{1}{q}\frac{d{J}_n}{dx}=(U-G)=0$ .
   这意味着 J_n 在整个耗尽区是恒定的。类似地，J_p 在整个耗尽区也是恒定的。
4. 突变或阶梯掺杂分布（N_A⁺, N_D⁺ 在各自区域中恒定）。
5. 所有掺杂剂均被电离（N_A⁺= N_A, N_D⁺ = N_D）。
6. 一维设备。

求解

唯一需要求解的方程是泊松方程，根据 n(x) 和 p(x) =0、突变的掺杂分布和电离的掺杂剂原子，泊松方程变为：

$\frac{dE}{dx}=\frac{\rho }{\epsilon }=\frac{q}{\epsilon }(-N_A+N_D)$

或  ,

其中  

ε₀ 是真空电容率，ε_s 是半导体中的电容率，-x_p 和 x_n 分别是 p 型侧和 n 型侧的耗尽区边缘，从两种材料之间的物理结开始测量。

于是电场强度就变为

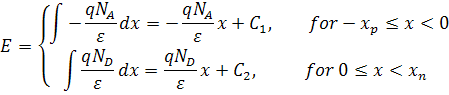
积分常数 C₁ 和 C₂ 可以通过使用耗尽区近似来确定，该近似指出电场强度在耗尽区边界处必须为零。从而得出：

 和

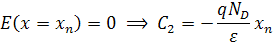
最大电场出现在 p 型和 n 型材料之间的结处。此外，我们知道电场线在界面上必须是连续的，这样 p 型侧和 n 型侧的电场在界面处或当 x = 0时必须相等。将 x = 0代入上述电场方程并将 E 的两个值设置为彼此相等，得出：N_Ax_p = N_Dx_n。该方程具有物理意义，因为它指出结一侧的总电荷必须与另一侧的总电荷相同。换句话说，如果电场被限制在耗尽区，那么II区的净电荷一定为零，因此负电荷和正电荷一定相等。 N_A x_p A 是总负电荷， N_A 是电荷密度，x_pA 是耗尽区的体积（A 是横截面积，x_p 是深度）。同样，N_D x_n A 是正电荷。横截面积 (A) 相同并相互抵消。

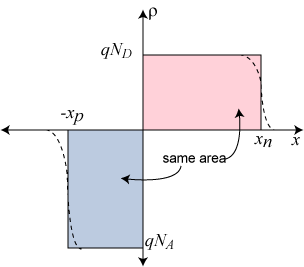
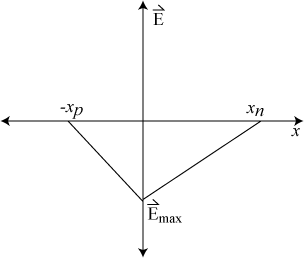
(a) pn 结中的掺杂浓度。虚线是实际的净电荷密度（尾部被夸大），实线表示耗尽区近似中假设的电荷密度。 (b) pn 结中的电场强度。

上图是我们开始时所讲的泊松方程的图示，其中电荷是电场的斜率：

为了找到电压与距离的函数关系，我们对电场方程进行积分。

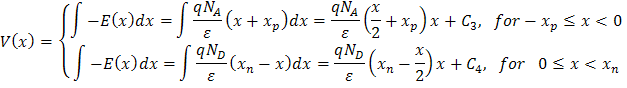
通常我们对结点处的电势差感兴趣，并且可以将任意一侧设为零。这里我们将 p 型侧的电压定义为零，这样在 x= -x_p 时，V=0。常数 C₃ 如下：

, 从而得到

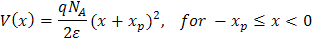
我们可以利用界面处n型侧和p型侧电势相同的事实来求得C₄，使得：

或 

V(x) 整合为：

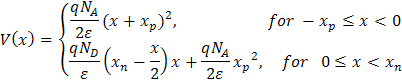
总电压如下图所示。

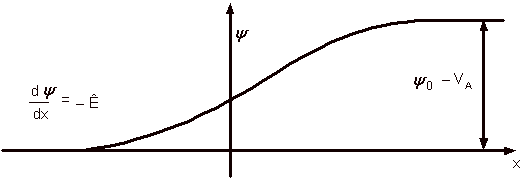
pn 结两端的电压图，假设 p 型侧的电压为零。

结点处的最大电压为 x= x_n，即：

该电压也等于 pn 结两端的内置电压 V₀（我们可以从 n 型材料和 p 型材料之间的费米能级差异中找到该电压），给出

在上面的等式中使用   并重新排列可以确定 x_p 和 x_n 。得到：

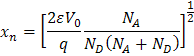and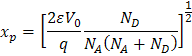

从这些方程我们可以得到最大电场强度：

,

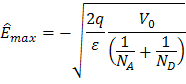和耗尽区的总宽度

 和 

其中 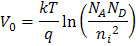 为内置电压，需单独计算。