计算总电流

概述

  1. 只有假设总电流在太阳能电池距离范围内恒定，没有注入或提取载流子的接触，并且电池在稳态条件下运行，才能计算总电流。
  2. 区域 I 和 II 中的电流已知，但两个区域的距离变量不同。因此，在求解总电流之前，我们必须考虑到这一点。
  3. 总电流 = 耗尽​​区边缘的电流（考虑距离变量差异后区域 I 和区域 II 中的电流）

为了求得总电流，我们注意到，只要不存在可以提取或注入载流子的接触并且只要器件处于稳态条件下，器件中的总电流必须恒定，与距离无关。表达式如下：

 

d J T d x = d ( J p + J n ) d x = d J p d x + d J n d x = − q ( U p + G p ) + q ( U n + G n ) = q ( G n − G p ) − q ( U n − U p )

 

由于每个电子产生一个空穴，每次复合时电子也消耗一个空穴，Un = Up，Gn = Gp，因此 JT 的导数为 0，JT 为常数。从物理上讲，连续性方程表明半导体中（稳态）电子和空穴的总数不能改变，因此总电流也不能改变。因此，如果我们在设备的任何地方求得了 JT，那么就等于我们在设备的任何地方都求得了它的值。而最方便的就是找到耗尽区边缘的总电流。由于我们知道 I 区和 III 区的电流，为了计算总电流，我们需要做两件事。 (1) 考虑距离变量 x 在区域 I 和区域 III 中不同的事实，并且 (2) 找到耗尽区边缘的电流。

使距离变量相同

在我们的解决方案中，上述方程中的距离变量 x 对于不同区域通常是不同的。通常，我们将区域 I（此处为具有电子少数载流子电流的 p 型区域）中的 x' 定义为距耗尽区边缘的距离，并随着深入区域 I而增加。另一个距离变量 x 定义为在另一个耗尽区处边缘为原点并随着深入区域 III 而增加（此处为具有空穴少数载流子电流的 n 型材料）。使用这些定义，传输方程为：

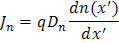and

因为 x = - x' - W ,

所以电流变为  或

耗尽区内电流

之前我们说过，耗尽区内生成为零，自由载流子数量很少，因此复合也可以忽略不计。如前面所述，在这些条件下，耗尽区的电流变化为零，我们可以用 I 区和 III 区边缘电流的总和来计算总电流，如下所示：

更准确的计算方法包括耗尽区中 Jn 和 Jp 的变化，我们通过以下方式找到总电流：

其中 ΔJp-dep 是耗尽区中 Jp 的变化。我们可以通过连续性方程计算 ΔJn-dep 

下面的连续性方程给出了电流与复合和生成的关系。

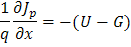
在耗尽区变为

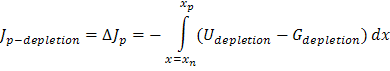
通常，复合项被忽略，G 被假设为常数，因此