Overview
- Total current can only be solved, assuming it is constant over the distance of the solar cell, if there is not a contact to inject or extract carriers and if the cell is operating under steady state conditions.
- Current in region I and II is known, but the distance variable is different for the two regions. Therefore we must take this into account before we solve for total current.
- Total current = current at depletion region edges (current in region I and region II after accounting for the distance variable difference).
To find the total current, we note that the TOTAL current in the device must be constant, independent of distance as long as there is not a contact that can extract or inject carriers and as long as the device is under steady state conditions. This can be shown by:
Since each electron generates a hole and each recombining electron also uses up a hole, Un = Up and Gn= Gp so that the derivative of JT is 0 and JT is a constant. Physically, the continuity equation is stating that the total number of electrons and holes cannot change in the semiconductor (in steady state), and hence the total current also cannot change. Therefore if we find JT anywhere in the device, we have found it everywhere in the device. It is most convenient to find the total current at the edges of the depletion regions. Since we know the currents in Regions I and III, to calculate the total current, we need to do two things. (1) Account for the fact that the distance variable x is not the same in Region I and Region III and (2) find the current at the depletion region edges.
Making the distance variable the same
In our solutions, the distance variable, x, in the above equations is usually not the same for the different regions of the device. Typically, we define x' in Region I (here p-type region with an electron minority carrier current) as the distance from depletion region edge and increasing further into Region I. The other distance variable x, is defined as zero at the other depletion region edge and is increasing into Region III (here n-type material with a hole minority carrier current). Using these definitions, the transport equations are:
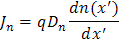 and
and ![]()
Since x = - x' - W , ![]()
and then the current becomes ![]() or
or
![]()
Current across the depletion region
Previously, we stated that the generation was zero and the number of free carriers was small, so the recombination could also be neglected the depletion region. As previously stated, under these conditions, the change in current across the depletion region is zero and we can find the total current just as the sum of the currents at the edges of Region I and III, as shown below:
![]()
A more accurate solution includes the change in Jn and Jp across the depletion region, and we find the total current by:
![]()
where ΔJp-dep is the change in Jp across the depletion region. We could solve for ΔJn-dep via the continuity
equation. The continuity equations, repeated below, give current dependence on recombination and generation.
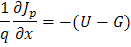
and in the depletion region this becomes
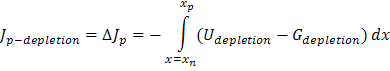
Often, the recombination term is ignored and G is assumed to be a constant, such that
![]()
