正午时的方位角和仰角是用于定位光伏组件的两个关键因素。但是，要计算一整天的太阳位置，必须一整天都要计算其仰角和方位角。这些角度是使用“太阳时间”计算的。在常规计时中，地球区域被划分为不同的时区。但是，在这些时区的某些位置上，中午并不一定与太阳在天空中最高的时刻相对应。同样，日出被定义为在时区中的某些位置上太阳升起的阶段。但是，由于一个时区所覆盖的面积广大，在时区的某个位置太阳实际出现在地平线上的时间可能与“定义的”日出时间（或正式公认的日出时间）完全不同。这种约定是必要的，否则相邻建筑的房屋在时间上其实也会相差几秒钟。另一方面，太阳时对于每个特定的经度都是唯一的。因此，要计算太阳的位置，首先要找到当地的太阳时，然后计算仰角和方位角。
地方太阳时（LST）和地方时（LT）
地方太阳时正午12点（LST）定义为当太阳在太空中最高的时刻。地方时（LT）通常与LST不同，这是因为地球轨道的离心率以及人为调整（例如时区和夏令制）的缘故。
地方标准时子午线（LSTM）
地方标准时子午线（LSTM）是用于特定时区的参考子午线，类似于用于格林威治标准时间的本初子午线。LSTM如下图所示。
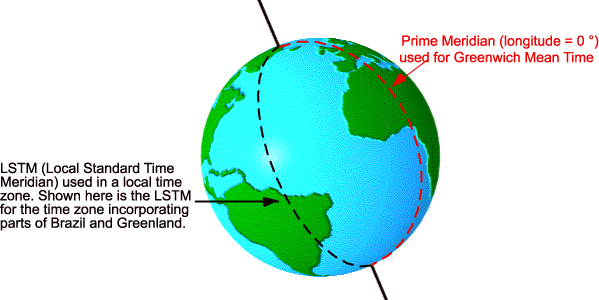
LSTM根据下列公式计算得出：
其中ΔTGMT是地方时（LT）与格林威治标准时间（GMT）的小时数差。
均时差（EoT）
均时差（EoT）（以分钟为单位）是一个经验方程式，用于校正地球轨道的偏心率和地轴倾斜。
其中
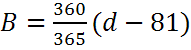
以度为单位，d为自年初以来的天数。时间校正EoT绘制在下图中。
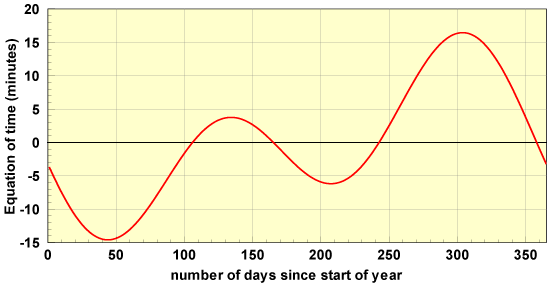
日晷将均时差作为图表包含其中，以提供全年正确的时间。其他时间校正要么合并到日规的设计中，要么以恒定的抵消量给出。
时间校正因子（TC）
净时间校正因子（以分钟为单位）考虑到了因为时区内经度变化导致的地方太阳时（LST）变化，并包含了上述EoT因素。
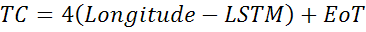
4分钟的因素是由于地球每4分钟自转1°的实际情况。
地方太阳时（LST）
可以通过对地方时（LT）使用前面描述的两项校正来找到地方太阳时（LST）。
时角（HRA）
时角用于将地方太阳时（LST）转换为太阳在天空中移动的度数。根据定义，时角在太阳正午为0°。由于地球每小时旋转15°，因此距太阳正午每过1小时对应于太阳在天空中的角运动为15°。早上时角为负值，下午为正值。
偏角
偏角公式如之前给出：
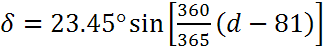
其中d是年初以来的天数。
仰角和方位角
仰角α，如下列页面所给出： https://www.pveducation.org/pvcdrom/properties-of-sunlight/elevation-angle
Elevation Angle
Azimuth
$$Azimuth=cos^{-1}[\frac{sin\delta cos\varphi-cos\delta sin \varphi cos(HRA)}{cos\alpha}]$$
其中φ是纬度。
太阳在全天中的位置
下页提供的计算器用于查找全年中任何位置的太阳仰角和方位角。
English
Español
한국어
Bahasa Indonesia