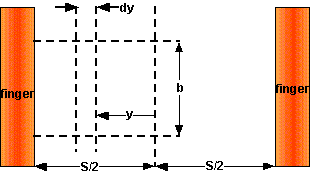
根据薄层电阻率，发射极电阻引起的功率损耗可以计算为顶部接触中排线间距的函数。然而，电流在发射极中流动的距离并不是恒定的。电流可以从靠近排线的基极收集，因此只有很短的距离流向排线，或者，如果电流进入排线之间的发射极，则这种载流子的电阻路径的长度为网格间距的一半。
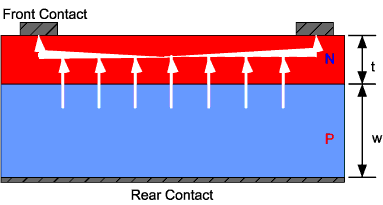
太阳能电池中从生成点到外部接触点的理想电流。发射极通常比图中所示的薄得多。
dy 部分的增量功率损耗由下式给出：
$$d P_{\text {loss}}=I^{2} d R$$
微分电阻由下式给出：
$$d R=\frac{\rho}{b} d y$$
其中
ρ 是薄层电阻率，单位为 Ω/sqr
b 是沿着排线的距离；和
y 两个网格排线之间的距离，如下所示。
计算顶层侧向电阻引起的功率损耗所需的规格。
电流还取决于 y，I(y) 是横向电流，在均匀照明下，横向电流在光栅线之间的中点处为零，并在光栅线处线性增加至最大值。电流方程为：
$$I(y)=J b y$$
其中
J 为电流密度；
b 是沿着排线的距离；和
y 两个网格排线之间的距离，如上所示。
因此，总功率损耗为：
$$P_{loss}=\int I(y)^{2} d R=\int_{0}^{S / 2} \frac{J^{2} b^{2} y^{2} \rho_{\square} d y}{b}=\frac{J^{2} b \rho_{\square} S^{3}}{24}$$
其中
S 是网格线之间的间距。
在最大功率点，产生的功率为：
$$P_{g e n}=J_{M P} b \frac{S}{2} V_{M P}$$
功率损耗部分由下式给出：
$$P_{\% \text { lost }}=\frac{P_{\text {loss}}}{P_{\text {gen}}}=\frac{\rho_{\mathrm{D}} S^{2} J_{M P}}{12 V_{M P}}$$
由此，可以计算顶部接触网格的最小间距。例如，对于典型的硅太阳能电池，其中 ρ = 40 Ω/sq、Jmp = 30 mA/cm2、Vmp = 450 mV，为了使发射极功率损耗小于 4%，排线间距应小于 4毫米。
English
Español