Based on the sheet resistivity, the power loss due to the emitter resistance can be calculated as a function of finger spacing in the top contact. However, the distance that current flows in the emitter is not constant. Current can be collected from the base close to the finger and therefore has only a short distance to flow to the finger or, alternatively, if the current enters the emitter between the fingers, then the length of the resistive path seen by such a carrier is half the grid spacing.
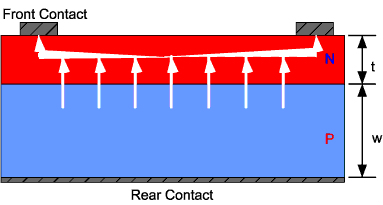
Idealised current flow from point of generation to external contact in a solar cell. The emitter is typically much thinner than shown in the diagram.
The incremental power loss in the section dy is given by:
$$d P_{\text {loss}}=I^{2} d R$$
The differential resistance is given by:
$$d R=\frac{\rho}{b} d y$$
where
ρ is the sheet resistivity in Ω/sqr
b is the distance along the finger; and
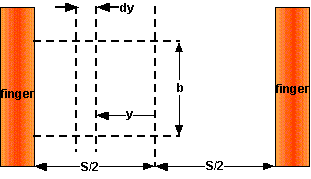
y the distance between two grid fingers as shown below.
Dimensions needed for calculating power loss due to the lateral resistance of the top layer.
The current also depends on y and I(y) is the lateral current flow, which is zero at the midpoint between grating lines and increases linearly to its maximum at the grating line, under uniform illumination. The equation for the current is:
$$I(y)=J b y$$
where
J is the current density;
b is the distance along the finger; and
y the distance between two grid fingers as shown above.
The total power loss is therefore:
$$P_{loss}=\int I(y)^{2} d R=\int_{0}^{S / 2} \frac{J^{2} b^{2} y^{2} \rho_{\square} d y}{b}=\frac{J^{2} b \rho_{\square} S^{3}}{24}$$
where
S is the spacing between grid lines.
At the maximum power point, the generated power is:
$$P_{g e n}=J_{M P} b \frac{S}{2} V_{M P}$$
The fractional power loss is given by:
$$P_{\% \text { lost }}=\frac{P_{\text {loss}}}{P_{\text {gen}}}=\frac{\rho_{\mathrm{D}} S^{2} J_{M P}}{12 V_{M P}}$$
Hence, the minimum spacing for the top contact grid can be calculated. For example, for a typical silicon solar cell where ρ= 40 Ω/sq, Jmp = 30 mA/cm2, Vmp = 450 mV, to have a power loss in the emitter of less than 4% the finger spacing should be less than 4 mm.