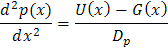计算准中性区域

根据耗尽区近似，在上一页的区域 I 和 III 中不存在电场。因此，泊松方程变为零，传输方程中的漂移项 (q μ _nnE or q μ _p pE ) 也变为零。准中性区中的少数载流子仅通过扩散来移动。

传输方程变为：

                   (1a)

                (1b)

连续性方程保持不变：

                      (2a)

               (2b)

	对于电子，对上面的 (1a) 求导并代入上面的 (2a) 得到	对于空穴，对上面的 (1b) 求导并代入上面的 (2b) 得到
	, 或	, 或
	(3a)	(3b)

只要耗尽区近似成立（假设低注入），并且漂移和扩散是仅有的传输方式，方程（3a）和（3b）在稳态条件下是通用的。对于稳态和低注入，必须求解这些方程才能确定器件 IV 方程的电气特性。这些二阶微分方程的解首先涉及找到 U 和 G 的方程以确定微分方程的通解，然后确定边界条件以找到特解。

少数载流子电流占主导地位

在区域 I 或区域 III 中，总电流由两个电流分量组成：J_n（由电子形成的电流）和 J_p（由空穴形成的电流）。然而，我们将仅求解每种材料中的少数载流子电流，因为少数载流子的复合控制着电流。稍后，我们还将基于总电流恒定的事实来计算多数载流子电流 J_p（p型材料中）。

求复合率：假设低注入

SRH 复合率的一般形式为：

其中n₁、p₁是复合处的载流子数量，n₀、p₀是平衡状态下的电子和空穴浓度，τ_p0和τ_n0是空穴和电子的少数载流子寿命。

在 p 型材料中，在低注入（低偏压）条件下，p >> n 同时 p ≈ p₀。此外，我们将假设 n >> n₁ 和 p >> p₁ 并且 n 型和 p 型材料的寿命没有显着变化（即 τ_n0p >> τ_p0n）。然后，对于 p 型材料中电子的复合率上式可简化为：

这是复合率的低注入形式，通常用于 pn 结的解析解方法，因为它大大简化了数学计算。

对于 n 型材料中的空穴，

求生成率：

一般而言，G 由以下等式给出：

其中 N₀ = 表面的光子通量（光子/单位面积/秒）；
α = 吸收系数；和
x = 进入材料的距离。

注意，N₀ 可以随时间变化并且可以随波长改变，即 N₀ 通常将是由 N₀(λ,t) 表示的关于时间和波长的函数，这也使得生成率 G 成为关于波长和时间的函数。然而，这里我们仅求解稳态并忽略任何时间依赖性。而波长依赖性通常通过将某一波长下求得的结果与其他所有我们关注的波长下的结果相加来得到。生成率的指数形式使得待求解的微分方程变为非齐次二阶微分方程。因此，对生成率的近似通常假设生成是恒定的（当其数值与 α-1 相比较小时有效），在表面存在脉冲生成，或者生成为零。

寻找通解

(3a) 和 (3b) 中微分方程的通解取决于 U 和 G 的方程。有几种常见的通解。如下所示，其中 是仅取决于 x 的任何函数，并且对于 pn 结方程 通常对应于 n(x)、p(x)、Δn(x) 或 Δp(x) 之一。 A 和 B 是需要由边界条件确定的常数。 C 和 K 是半导体或器件常数。 对pn 结方程来说 C 通常是 L_n 或 L_p（少数载流子扩散长度），K 通常是常数生成项 G。

微分方程的形式	通解	何时使用
		体复合，无生成
		体复合，稳定生成
		复合与生成为零
		零复合，稳定生成

找到特解（所有方程应用于 p 型材料中的电子）

特解方案取决于每个区域或区域两侧边缘的情况。对于许多半导体器件，至少一个边缘将是pn结，因此下面的边界条件适用于许多半导体器件。

1. pn 结耗尽区边缘的边界条件：
   p型材料中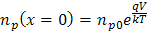： or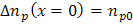
   n型材料中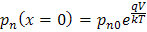： or
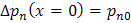
2. 半导体表面可能的边界条件

   其他边界条件可能取决于器件的表面。表面复合速度 S_r 决定了表面的条件。下面列出了 p 型材料的一些常见表面边界条件。

   表面位置	边界描述	方程
   表面远离结点 (W>>Ln)	少数载流子浓度必须是有限的，当 x -> ∞	n(x->∞) = finite
   表面位于结点的几个扩散长度范围内	表面复合“无限”快 (Sr = ∞) 。所有到达表面的载流子都会复合。	Δn (x=W) = 0
   表面位于结点的几个扩散长度范围外	表面复合是有限的。
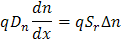
   靠近发光源的表面	在表面产生脉冲光，无表面复合

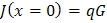
求解 I 区和 III 区的扩散电流

一旦我们从 2(b) 和 2(c) 中描述的过程中得到 n(x) 和 p(x) 的形式，我们就可以使用通用方程轻松求得少数载流子电流：

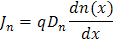and