Descripción general
- Los principales supuestos son: la aproximación de agotamiento, la falta de portadores libres en esta región y la concentración de dopantes es constante.
- Partiendo de estas premisas, se puede utilizar la ecuación de Poisson para desarrollar una solución para la región de agotamiento.
- Se puede resolver tanto el campo eléctrico máximo y la anchura total agotamiento.
Como se ha indicado en la página anterior tenemos que hacer ciertas hipótesis para resolver las ecuaciones de diodos analíticamente.
Las hipótesis son:
- La aproximación de agotamiento: el campo eléctrico se limita a la región de la unión y no hay campo eléctrico en las regiones cuasi neutral.
- No hay portadores libres (n(x), p(x) = 0 ) en la región de agotamiento.
- Podemos asumir que no hay portadores libres ya que el campo eléctrico los arrastra fuera de la región de agotamiento rápido. La inexistencia de portadores libres significa que (1) las ecuaciones de transporte no sirven y (2) que no hay recombinación o generación, por lo que la ecuación de continuidad se convierte en
.
Esto significa que Jn es constante en toda la región de agotamiento. Del mismo modo, Jp es también constante en toda la región de agotamiento. - .Abrupto perfil de dopaje (NA+, ND+ son constantes en sus respectivas regiones).
- Todos los dopantes son ionizados (NA+= NA, ND+ = ND).
- El dispositivo es unidimensional.
Solución
La única ecuación que queda por resolver es la ecuación de Poisson, con n(x) y p(x) =0, un perfil de dopaje abrupto y los átomos dopantes ionizados. La ecuación de Poisson se convierte en:
o ![]() ,
,
dónde 
ε0 es la permitividad del espacio libre, y εs es la permitividad en el semiconductor y -xp y xn son los bordes de la región de agotamiento en el lado P y N, respectivamente, medida desde la unión física entre los dos materiales.
El campo eléctrico se convierte entonces
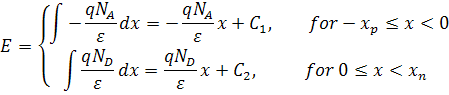
La integración de las constantes C1 y C2 se pueden determinar mediante el uso de la aproximación de agotamiento, que establece que el campo eléctrico debe ir a cero en el límite de las regiones de agotamiento. Esto da:
![]() y
y
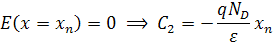
El campo eléctrico máximo se produce en la unión entre el material de tipo p- y de tipo n. Además, se sabe que las líneas de campo eléctrico deben ser continuas a través de la interfaz, el campo eléctrico en el lado de tipo p y el lado de tipo n debe ser igual entre sí, en la interfaz o cuando x = 0. poniendo x = 0 en la ecuación anterior para el campo eléctrico y estableciendo los dos valores de E iguales entre sí, da: NAxp = NDxn. Esta ecuación tiene sentido físico, ya que indica que la carga total en un lado de la unión debe ser la misma que la carga total en el otro. En otras palabras, si el campo eléctrico se limita a la región de agotamiento, la carga neta en la Región II debe ser cero, y, por lo tanto, la carga negativa y la carga positiva deben ser igual. NA xp A es la carga negativa total, ya que NA es la densidad de carga y xpA es el volumen de la región de agotamiento (A es el área de sección transversal y xp es la profundidad). Del mismo modo, ND xn A es la carga positiva. El área de sección transversal (A) es el mismo y se anula.
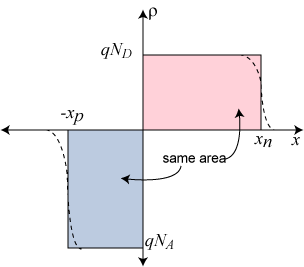
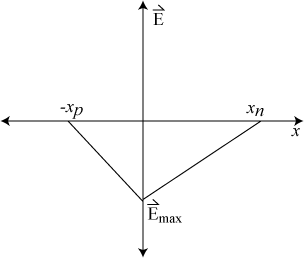
(a) La concentración del dopaje en una unión pn. Las líneas discontinuas son la densidad de carga neta real (las colas son exageradas) y la línea continua representa la densidad de carga asumida en la aproximación de agotamiento. (b) El campo eléctrico en una unión pn.
Los gráficos anteriores son una ilustración de la ecuación de Poisson que empezamos con el lugar donde la carga es la pendiente en la gráfica del campo eléctrico:
Possion's Equation (simple)
Para encontrar la tensión en función de la distancia, integramos la ecuación para el campo eléctrico.
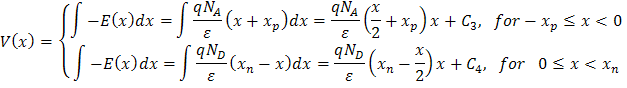
Estamos por lo general interesado en la diferencia de potencial a través de la unión y se puede establecer arbitrariamente un lado a cero. Aquí se define el voltaje en el lado de tipo p como cero, de tal manera que en x= −xp, V=0. Esto de el constante C3 como:
![]() , lo que da
, lo que da
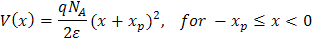
podemos encontrar C4 utilizando el hecho de que el potencial en el lado de tipo n y el lado de tipo p son idénticos en la interfaz, tal que:
![]()
o ![]()
En general, V(x) es:
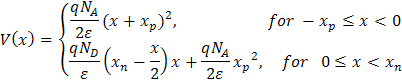
El voltaje total se representa a continuación.
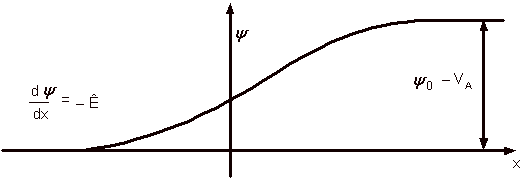
Representación de la tensión a través de una unión pn, suponiendo que la tensión en el lado de tipo p es cero.
La tensión máxima a través de la unión es una x= xn, que es:
![]()
Este voltaje es también igual a la tensión incorporada través de la unión pn, V0, (que podemos encontrar a partir de la diferencia en los niveles de Fermi-entre los materiales de tipo n y de tipo), dando
![]()
El uso de ![]() en la ecuación anterior y su reordenación, permite determinar xp y xn. Estos son:
en la ecuación anterior y su reordenación, permite determinar xp y xn. Estos son:
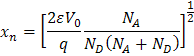 y
y 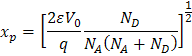
A partir de estas ecuaciones podemos obtener el campo eléctrico máximo
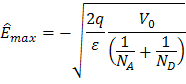 ,
,
y la anchura total de la región de agotamiento
Ideal Diode - width of the depletion region
![]() y
y ![]()
Dónde 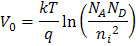 es el potencial o voltaje de contacto y se calcula por separado.
es el potencial o voltaje de contacto y se calcula por separado.
