Para un módulo en una inclinación y orientación arbitraria la ecuación se vuelve un poco más complicada:
Solar Intensity
α es el ángulo de elevación del sol y Θ es el ángulo de azimuth del sol. β es el ángulo de inclinación del módulo. Un módulo acostado en el suelo tiene β =0° y un módulo vertical, tiene β =90°. Ψ es el ángulo de acimut que el módulo se enfrenta. La inmensa mayoría de los módulos están alineados de cara hacia el ecuador. Un módulo en el hemisferio sur se enfrentará al norte con Ψ = 0° y un módulo en el hemisferio norte generalmente se enfrentará directamente al sur con Ψ = 180°. Smódulo and Sincidente , respectivamente, las intensidades de luz en el módulo y de la luz entrante en W/m², siendo el Sincident el único componente directo.
Un módulo que se enfrenta directamente al sol de manera que los rayos entrantes son perpendiculares a la superficie del módulo tiene el módulo de inclinación igual al ángulo cenital del sol (90 - α = β), y, también, el ángulo de azimut del módulo igual al ángulo de azimut del sol (Ψ = Θ).
Los siguientes cálculos combinan el cálculo de la posición del sol con la fórmula de la masa de aire y luego se calcula la intensidad de la luz incidente en un módulo con inclinación y orientación arbitraria.
Light Intensity
Utilizando Vectores para Calcular la Dirección Solar
Cuando el número de inclinaciones y orientaciones es más complicado, es más fácil convertir a vectores las direcciones solares de azimut y elevación. Un ejemplo es donde hay un módulo inclinado en un edificio que también está en una inclinación y orientación arbitraria. La simplicidad de la utilización del vector viene del hecho de que la reducción en la intensidad de la luz sobre una superficie inclinada es simplemente el producto escalar entre el rayo incidente y la normal al módulo.
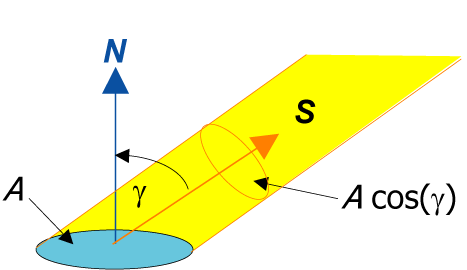
La luz que incide sobre una superficie en un ángulo determinado se extiende sobre un área mayor. La reducción en la intensidad es el producto escalar de los vectores unitarios S y N
Solar Intensity Vector
dónde Smódule and Sincidente son como se definieron antes y S es el vector unitario apuntando hacia el sol y N es el vector unitario normal a la superficie del módulo. γ es el ángulo entre los dos vectores.
