Diffusion

El movimiento aleatorio constante de portadores puede conducir a un movimiento neto de los portadores si una región en particular tiene una mayor concentración de portadores que otra región (un gradiente de concentración entre la región de alta concentración de portadores y la región de baja concentración de portadores). Por tanto, el movimiento neto de portadores va de las zonas de alta concentración a las de baja. Si dejamos actuar a este movimiento aleatorio, con el tiempo, los portadores se distribuirán uniformemente en el espacio a través del movimiento al azar. Esto se puede ver en la animación debajo.

La velocidad a la que se produce la difusión depende de la velocidad a la que los portadores se mueven y de la distancia entre los eventos de dispersión. Se denomina difusividad y se mide en cm²s^-1.Los valores para el silicio, el material semiconductor más utilizado para las células solares, se dan en el apéndice. Debido a que elevando la temperatura aumentará la velocidad térmica de los portadores, la difusión se produce más rápido a temperaturas más altas.

Un efecto importante de la difusión es que, con el tiempo, se nivela las concentraciones de portadores en un dispositivo, como los inducidos por generación y recombinación, si ninguna fuerza externa se aplica al dispositivo. Esto se muestra en la siguiente animación en la que una región del dispositivo tiene una alta concentración de electrones y el otro tiene una alta concentración de huecos. Debido al movimiento puramente aleatorio de los portadores, las dos concentraciones serán uniformes en todo el material, con el paso del tiempo.

Los huecos (azul) y los electrones (rojo) se desplazan desde las zonas de alta concentración a baja concentración en un semiconductor hacia una distribución uniforme. Los huecos (de color azul) tienen una difusividad menor que los electrones (de color rojo), por lo que necesitan más tiempo para llenar el espacio completo.

Difusión Ecuación Derivación

Se conoce por la física molecular que el flujo de difusión de partículas es proporcional al gradiente de concentración.

Ecuaciones de difusión unidimensionales

Para los electrones (n) y huecos (p) se puede escribir como:

,

dónde: 

J_n y J_p = las densidades de corriente de difusión

q = carga del electrón

D_n y D_p  =  coeficientes de difusión para electrones y huecos

n y p  =concentraciones de electrones y huecos

La ecuación de la difusión de los portadores en el volumen de los semiconductores

Con el tiempo (t1, t2, t3), un pulso inicial de electrones se difundirá.

Esparcimiento de un pulso de electrones por difusión. La parte arbitraria de n(x) se divide en los segmentos de longitud igual al recorrido libre medio de los electrones. La concentración se supone que es constante para cada segmento.

Velocidad de difusión de electrones en semiconductores =
Densidad de flujo de electrones =número de electrones que pasan por x_o por unidad de tiempo y área

Considere la posibilidad de pequeños segmentos, l,a la izquierda y derecha de x₀ y las concentraciones de electrones n₁ y n₂ en estos segmentos como aproximadamente uniformes.

Por lo tanto, la densidad de flujo de electrones de izquierda a derecha =

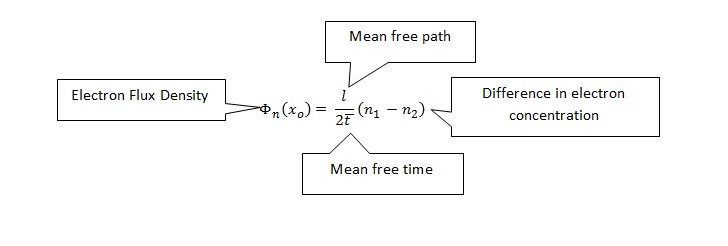
La diferencia en la concentración de electrones entre los dos puntos (n₁ and n₂) debe ser descrito en términos entendibles. Podemos definir tanto n₁ and n₂ utilizando un extracto de la gráfica anterior.

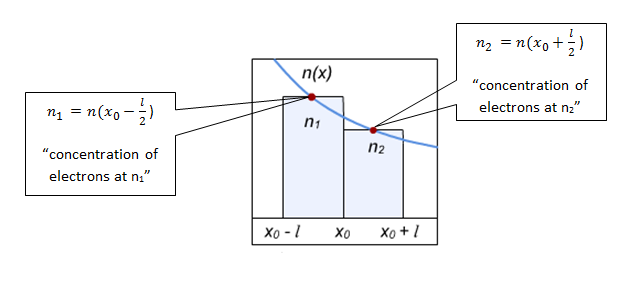
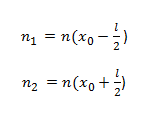
Suponemos que l es muy pequeña, y por lo tanto, podemos usar la pendiente en x_o con el fin de determinar la concentración de electrones (n) at x_o ±

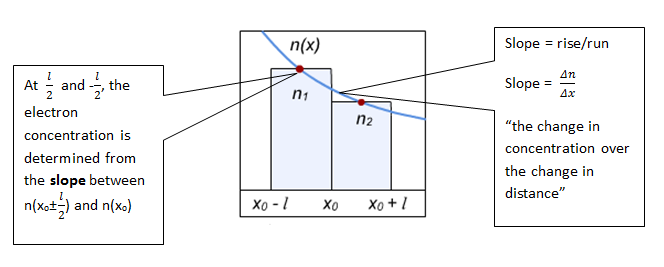
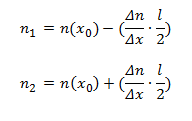
Substituyendo:

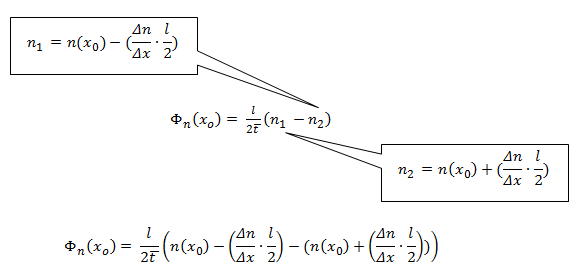
Simplificando:

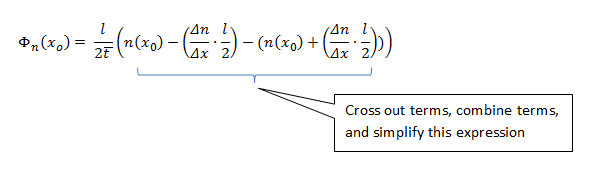
Cancelando términos:

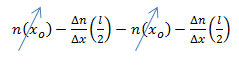
Combinando términos:

Simplificando:

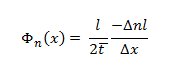
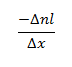
Substituyendo en la ecuación original:

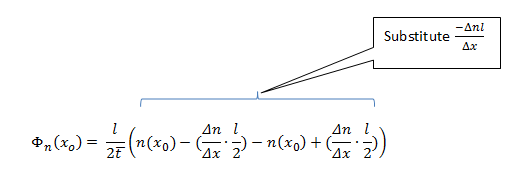
Combinando los términos de l:

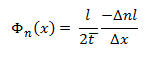
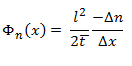
Con el fin de aproximarse a la concentración de electrones cuando x cambia, supongamos que x es muy pequeño.
Para ello, tomamos el límite cuando x → 0

Mueva las constantes delante del límite:

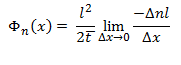
Tome el límite:

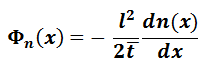
*Esta derivación puede ser utiliza también para huecos!

Redefina las constantes y la ecuación para los electrones:

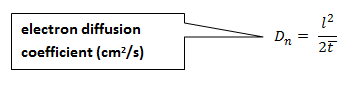
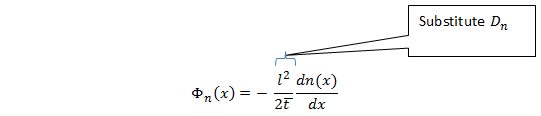
PARA ELECTRONES:

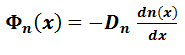
D_n es el coeficiente de difusión de electrones con unidades cm²/s. El signo menos surge del hecho de que el vector del gradiente de la concentración se dirige hacia el aumento de la concentración, mientras que las partículas se difunden a la zona con concentración más baja.

La dirección del gradiente de concentración es opuesto a la dirección del movimiento de los portadores con el resultado de que la fórmula de la densidad de flujo de portadores debe tener un signo negativo.

Ahora, redefina las constantes y la ecuación para los huecos:

Substituya:

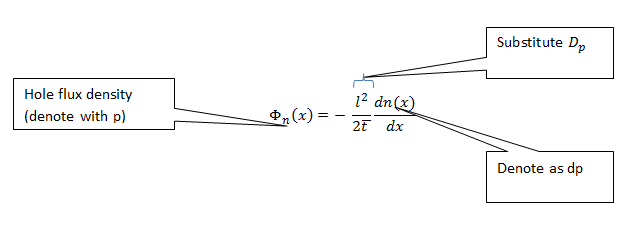
Para HUECOS:

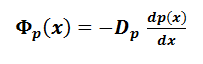
Densidad de corriente de difusión= densidad de flujo de portadores multiplicada por la carga del portador (denominada q)

Para Electrones:

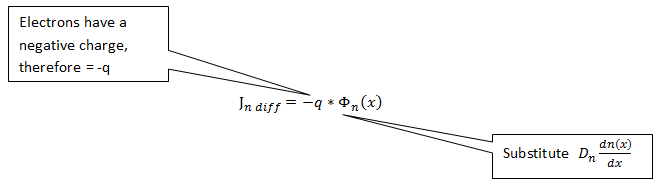
Simplificando:

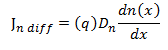
Para huecos:

Información general:

Ecuación de Continuidad

Las ecuaciones de continuidad definen la velocidad de crecimiento de los portadores en el volumen del semiconductor.

,

dónde U es la tasa de recombinación del portador, G - tasa de generación.

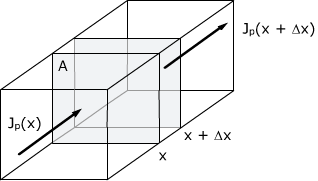
Corrientes entrando y saliendo el volumen AΔx.

Tenga en cuenta la longitud dx de los semiconductores y el movimiento de los huecos a través de él. El aumento neto de la concentración de huecos por unidad de tiempo es la diferencia entre el flujo de huecos que entran y salen del volumen AΔx más la tasa de generación y menos la tasa de recombinación.

En la forma derivada

,

Por último, substituyendo en las ecuaciones de la difusión se puede obtener

,