The spectral response is conceptually similar to the quantum efficiency. The quantum efficiency gives the number of electrons output by the solar cell compared to the number of photons incident on the device, while the spectral response is the ratio of the current generated by the solar cell to the power incident on the solar cell. A spectral response curve is shown below.
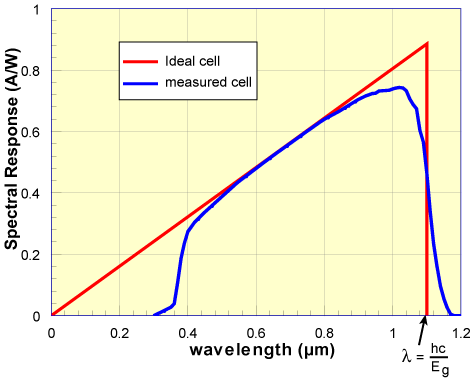
The spectral response of a silicon solar cell under glass. At short wavelengths below 400 nm the glass absorbs most of the light and the cell response is very low. At intermediate wavelengths, the cell approaches the ideal. At long wavelengths, the response falls back to zero. Silicon is an indirect band gap semiconductor so there is not a sharp cut off at the wavelength corresponding to the band gap (Eg = 1.12 eV).
The ideal spectral response is limited at long wavelengths by the inability of the semiconductor to absorb photons with energies below the band gap. This limit is the same as that encountered in quantum efficiency curves. However, unlike the square shape of QE curves, the spectral response decreases at small photon wavelengths. At these wavelengths, each photon has a large energy, and hence the ratio of photons to power is reduced. Any energy above the band gap energy is not utilised by the solar cell and instead goes to heating the solar cell. The inability to fully utilize the incident energy at high energies, and the inability to absorb low energies of light represents a significant power loss in solar cells consisting of a single p-n junction.
Spectral response is important since it is the spectral response that is measured from a solar cell, and from this the quantum efficiency is calculated. The quantum efficiency can be determined from the spectral response by replacing the power of the light at a particular wavelength with the photon flux for that wavelength. This gives:
$$SR=\frac{q \lambda}{h c} QE$$
- Log in or register to post comments
- 1 comment(s)
