The azimuth angle and the elevation angle at solar noon are the two key angles which are used to orient photovoltaic modules. However, to calculate the sun's position throughout the day, both the elevation angle and the azimuth angle must be calculated throughout the day. These angles are calculated using "solar time". In conventional time keeping, regions of the Earth are divided into certain time zones. However, in these time zones, noon does not necessarily correspond to the time when the sun is highest in the sky. Similarly, sunrise is defined as the stage when the sun rises in one part of the time zone. However, due to the distance covered in a single time zone, the time at which the sun actually clears the horizon in one part of the time zone may be quite different to the "defined" sunrise (or what is officially recognized as the time of sunrise). Such conventions are necessary otherwise a house one block away from another would actually be different in time by several seconds. Solar time, on the other hand is unique to each particular longitude. Consequently, to calculate the sun's position, first the local solar time is found and then the elevation and azimuth angles are calculated.
Local Solar Time (LST) and Local Time (LT)
Twelve noon local solar time (LST) is defined as when the sun is highest in the sky. Local time (LT) usually varies from LST because of the eccentricity of the Earth's orbit, and because of human adjustments such as time zones and daylight saving.
Local Standard Time Meridian (LSTM)
The Local Standard Time Meridian (LSTM) is a reference meridian used for a particular time zone and is similar to the Prime Meridian, which is used for Greenwich Mean Time. The LSTM is illustrated below.
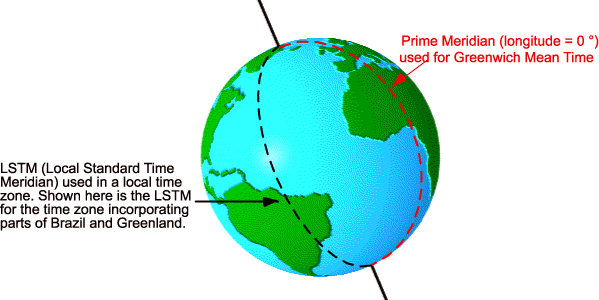
The (LSTM) is calculated according to the equation:
![]()
where ΔTGMT is the difference of the Local Time (LT) from Greenwich Mean Time (GMT) in hours.
Equation of Time (EoT)
The equation of time (EoT) (in minutes) is an empirical equation that corrects for the eccentricity of the Earth's orbit and the Earth's axial tilt.
![]()
where
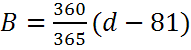
in degrees and d is the number of days since the start of the year. The time correction EoT is plotted in the figure below.
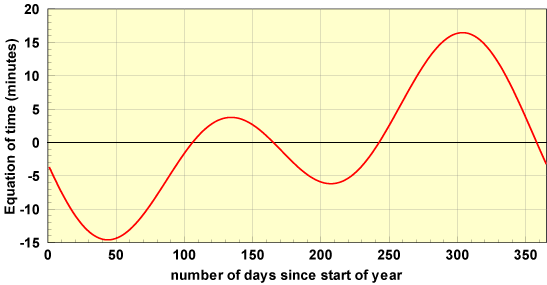
Sundials include the equation time as a table to provide the correct time throughout the year. The other time corrections are either incorporated into the design of the sundial or given as a constant offset.
Time Correction Factor (TC)
The net Time Correction Factor (in minutes) accounts for the variation of the Local Solar Time (LST) within a given time zone due to the longitude variations within the time zone and also incorporates the EoT above.
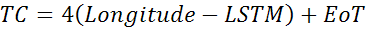
The factor of 4 minutes comes from the fact that the Earth rotates 1° every 4 minutes.
Local Solar Time (LST)
The Local Solar Time (LST) can be found by using the previous two corrections to adjust the local time (LT).

Hour Angle (HRA)
The Hour Angle converts the local solar time (LST) into the number of degrees which the sun moves across the sky. By definition, the Hour Angle is 0° at solar noon. Since the Earth rotates 15° per hour, each hour away from solar noon corresponds to an angular motion of the sun in the sky of 15°. In the morning the hour angle is negative, in the afternoon the hour angle is positive.
![]()
Declination
The declination angle has been previously given as:
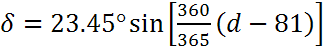
Where d is the number of days since the start of the year.
Elevation and Azimuth
The elevation, α, is described on page: https://www.pveducation.org/pvcdrom/properties-of-sunlight/elevation-angle
Elevation Angle
Azimuth
$$Azimuth=cos^{-1}[\frac{sin\delta cos\varphi-cos\delta sin \varphi cos(HRA)}{cos\alpha}]$$
where: φ is the latitude.
Sun's position throughout the day
A calculator to find the elevation and azimuth throughout the year at any location is given on the following page.
- Log in or register to post comments
- 5 comment(s)
 Español
Español 한국어
한국어 简体中文
简体中文 Bahasa Indonesia
Bahasa Indonesia
