Surface Recombination

The surface also plays an important role in recombination. Typically the surfaces complicate the measurement of the bulk lifetime. Recombination at the surfaces is typically described by a surface lifetime τ_s, which includes the fundamental decay mode but ignores higher decay modes. τ_s is a function of the surface recombination velocities S₁ and S₂, the cell width W and the minority carrier diffusivity D. The precise solution is quite complicated but approximate solutions exist for special cases and are sufficiently accurate for most purposes 1.

The simplified formulas given below can be used for transient measurements when the effective lifetime is much greater than the transient surface lifetime (). The more exact expression 2 3in transient measurements that works in all cases is:

$$ S = \sqrt{D \left(\frac{1}{\tau_{eff}}- \frac{1}{\tau_b}\right)} \tan  \left[\frac{W}{2} \sqrt{\frac{1}{D}\left(\frac{1}{\tau_{eff}}- \frac{1}{\tau_b}\right)}\right]$$

For quasi-steady-state measurements, the formulas are accurate if .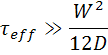

There is a list of approximate solutions for several important cases below:

Silicon wafer with a thickness of W

The surfaces are identical so S = S₁ = S₂.

One surface is perfectly passivated so S₂ = 0.

Both surfaces are perfectly passivated so S₁ = S₂ = 0.

Both surface have high recombination so S₁ and S₂ are large.

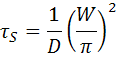
One surface has a high recombination and the other has a low recombination so S₁ = 0 and S₂ = ∞

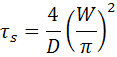
Effective Lifetime

The combination of the effects of surface and bulk recombination give the effective lifetime of carriers τ_eff within a sample.

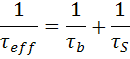
For many measurements, it is possible to reduce surface recombination of the surfaces to a low enough value so that τ_b ≫ τ _eff. Alternatively, if τ_b is sufficiently high the lifetime measurement is completely dominated by the surfaces and τ_s ≫ τ_eff. An accurate measurement of surface recombination is then possible.

• 1. A. B. Sproul, “Dimensionless solution of the equation describing the effect of surface recombination on carrier decay in semiconductors”, Journal of Applied Physics, vol. 76, pp. 2851-2854, 1994.
• 2. K. L. Luke and Cheng, L. - J., “Analysis of the interaction of a laser pulse with a silicon wafer: Determination of bulk lifetime and surface recombination velocity”, Journal of Applied Physics, vol. 61, pp. 2282-2293, 1987.
• 3. J. Brody and Rohatgi, A., “Analytical approximation of effective surface recombination velocity of dielectric-passivated p-type silicon”, Solid-State Electronics, vol. 45, no. 9, pp. 1549 - 1557, 2001.