Like all other semiconductor devices, solar cells are sensitive to temperature. Increases in temperature reduce the bandgap of a semiconductor, thereby effecting most of the semiconductor material parameters. The decrease in the band gap of a semiconductor with increasing temperature can be viewed as increasing the energy of the electrons in the material. Lower energy is therefore needed to break the bond. In the bond model of a semiconductor bandgap, a reduction in the bond energy also reduces the bandgap. Therefore increasing the temperature reduces the bandgap.
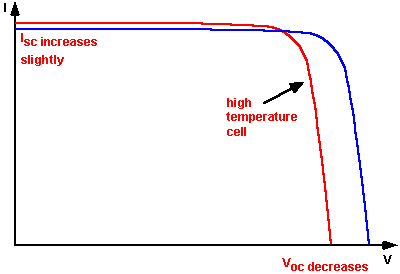
In a solar cell, the parameter most affected by an increase in temperature is the open-circuit voltage. The impact of increasing temperature is shown in the figure below.
The effect of temperature on the IV characteristics of a solar cell.
The open-circuit voltage decreases with temperature because of the temperature dependence of I0. The equation for I0 from one side of a p-n junction is given by;

where:
q is the electronic charge given in the constants page;
A is the area;
D is the diffusivity of the minority carrier given for silicon as a function of doping in the Silicon Material Parameters page;
L is the minority carrier diffusion length;
ND is the doping; and
ni is the intrinsic carrier concentration given for silicon in the Silicon Material Parameters page.
In the above equation, many of the parameters have some temperature dependence, but the most significant effect is due to the intrinsic carrier concentration, ni. The intrinsic carrier concentration depends on the bandgap energy (with lower bandgaps giving a higher intrinsic carrier concentration), and on the energy which the carriers have (with higher temperatures giving higher intrinsic carrier concentrations). The equation for the intrinsic carrier concentration is;
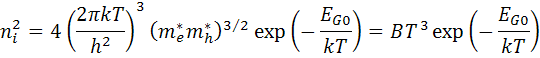
where:
T is the temperature;
h and k are constants given in the constants page;
me and mh are the effective masses of electrons and holes, respectively;
EGO is the bandgap linearly extrapolated to absolute zero; and
B is a constant which is essentially independent of temperature.
Substituting these equations back into the expression for I0, and assuming that the temperature dependencies of the other parameters can be neglected, gives;
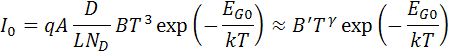
where B' is a temperature independent constant. A constant, γ, is used instead of the number 3 to incorporate the possible temperature dependencies of the other material parameters. For silicon solar cells near room temperature, I0 approximately doubles for every 10 °C increase in temperature.
VOC
The impact of I0 on the open-circuit voltage can be calculated by substituting the equation for I0 into the equation for Voc as shown below;
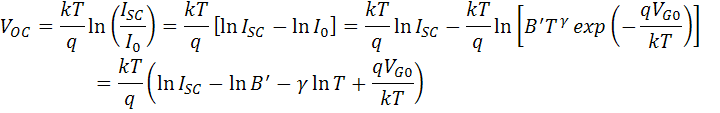
where EG0 = qVG0. Assuming that dVoc/dT does not depend on dIsc/dT, dVoc/dT can be found as;
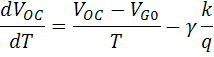
The above equation shows that the temperature sensitivity of a solar cell depends on the open-circuit voltage of the solar cell, with higher voltage solar cells being less affected by temperature. For silicon, EG0 is 1.2, and using γ as 3 gives a reduction in the open-circuit voltage of about 2.2 mV/°C;
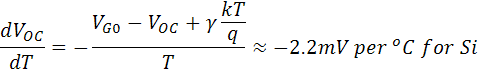
An alternate approach to determining VOC with temperature is from the variation of ni with temperature. We have seen that:
$$V_{OC}=\frac{n k T}{q} \ln \left(\frac{I_{L}}{I_{0}}+1\right)$$
IL has very small change with temperature when compared to I0 so changes in IL can be ignored. Further, changes in ni with temperature dominate the changes in I0. We can define a constant, A that includes recombination parameters that do not change with temperature so that at a temperature of T1:
$$I_0 = A n_i^2, and$$
$$V_{OC1}=\frac{k T_1}{q} \ln \left(\frac{I_{L}}{A n_i^2}\right)$$
$$A = \frac{I_L}{n_i^2e^\frac{qV_{OC1}}{kT_1}}$$
The previous three equations are at a fixed temperature such as 25 °C, but A is defined as constant across all temperature ranges.
In silicon, changes of n_i with temperature are approximated by1:
$$n_i = 9.38e19 \left (\frac{T}{300}\right )^2 e^\frac{-6884} {T}$$
Substituting ni into the equation for VOC gives:
$$V_{OC}=\frac{n k T}{q} \ln \left(\frac{I_{L}}{A \cdot 9.38e19^2 \left (\frac{T}{300}\right )^4 e^\frac{-2 \cdot 6884} {T}}\right)$$
Differentiating with respect to T gives:
$$\frac{dV_{oc}}{dT} = \frac{k}{q} \left [\ln \left(\frac{I_{L}}{A \cdot 8.798e39 \left (\frac{T}{300}\right )^4 }\right) -4 \right ]$$
Substituting for A in the equation above and simplifying gives:
$$\frac{dV_{oc}}{dT} = \frac{k}{q} \left \{ ln\left [ \left( \frac{T_1}{300} \right )^4 \right ]- \left(\frac{13768}{T_1} \right) -4 \right \} - \frac{V_{OC}}{T_1}$$
Typically T_1 is at 300 K (close to 25 °C) giving the result:
$$\frac{dV_{oc}}{dT} = -0.0043 + \frac{V_{oc1}}{300}$$
where dVOC/dT is in V/°C.
The result in the previous equation assumes that changes in VOC with temperature are entirely due to the changes in the intrinsic carrier concentration, ni. In reality, carrier lifetime, diffusivity change etc. also with temperature. The plot below shows the reported change in temperature of photovoltaic modules in the California Electric Commision module database as a function of cell VOC. The result from the change in ni alone is close to the average of the module set. There does not appear to be a systematic departure from the predicted values, indicating the variation is likely experimental error rather than changes in cell technology. The values are also self-reported by module manufacturers.
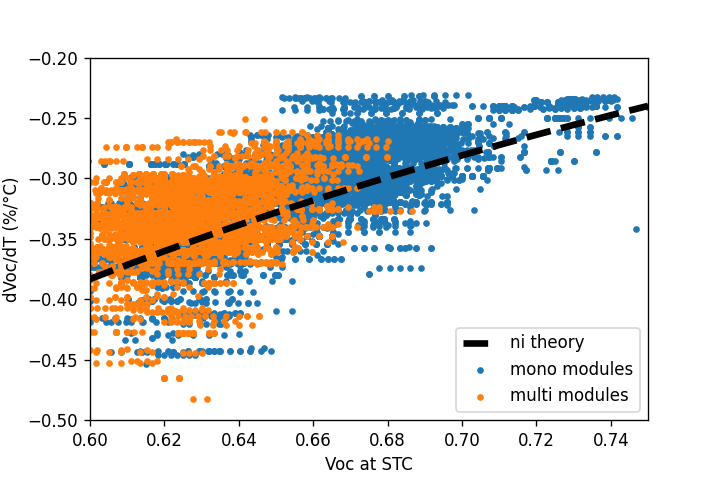
Change in Voc with temperature as reported in the CEC module database compared with the prediction from ni change with temperature.
ISC
The short-circuit current, Isc, increases slightly with temperature since the bandgap energy, EG, decreases and more photons have enough energy to create e-h pairs. However, this is a small effect, and the temperature dependence of the short-circuit current from a silicon solar cell is typically;
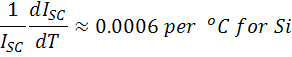
or 0.06% per °C for silicon.
The change of ISC with temperature is more dependent upon the design of the cell than the semiconductor material properties. A lower performance cell with little light trapping and a poor performance in long wavelengths near the band edge will have very little change in ISC with temperature. Conversely, a cell with a high response near the band edge will see a much larger change in ISC with temperature. In either case, the change of ISC with temperature is smaller than the change of VOC.
The temperature dependency FF for silicon is approximated by the following equation;
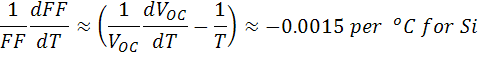
The effect of temperature on the maximum power output, Pm, is;


or 0.4% to 0.5% per °C for silicon.
300 K or 25 °C ?
Most semiconductor modeling is done at 300 K since it is close to room temperature and a convenient number. However, solar cells are typically measured almost 2 degrees lower at 25 °C (298.15 K). In most cases, the difference is insignificant (only 4 mV of Voc), and both are referred to as room temperature. Occasionally, the modeled results need to be adjusted to correlate with the measured results.
At 300 K, ni = 1.01 x 1010 cm-3 and kT/q = 25.852 mV
At 25 °C (298.15 K), ni = 8.6 x 109 cm-3 and kT/q = 25.693 mV
Measuring solar cell efficiency in Antarctica. Solar cells love cold sunny environments. (Photo Antony Schinckel)
- 1. , “Improved value for the silicon intrinsic carrier concentration from 275 to 375 K”, Journal of Applied Physics, vol. 70, pp. 846-854, 1991.
- Log in or register to post comments
- 3 comment(s)
 Español
Español 简体中文
简体中文