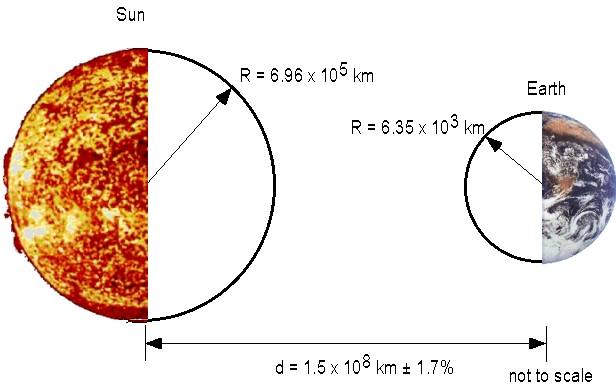
The solar radiation outside the earth's atmosphere is calculated using the radiant power density (Hsun) at the sun's surface (5.961 x 107 W/m2), the radius of the sun (Rsun), and the distance between the earth and the sun. The calculated solar irradiance at the Earth's atmosphere is about 1.36 kW/m2. The geometrical constants used in the calculation of the solar irradiance incident on the Earth are shown in the figure below.
Geometrical constants for finding the Earth's solar irradiance. The diameter of the Earth is not needed but is included for the sake of completeness.
The actual power density varies slightly since the Earth-Sun distance changes as the Earth moves in its elliptical orbit around the sun, and because the sun's emitted power is not constant. The power variation due to the elliptical orbit is about 3.4%, with the largest solar irradiance in January and the smallest solar irradiance in July. An equation 1 which describes the variation throughout the year just outside the earth's atmosphere is:
$$\frac{H}{H_{constant }}=1+0.033 \cos \left(\frac{360(n-2)}{365}\right)$$
where:
H is the radiant power density outside the Earth's atmosphere (in W/m2);
Hconstant is the value of the solar constant, 1.353 kW/m2; and
n is the day of the year.
These variations are typically small and for photovoltaic applications the solar irradiance can be considered constant. The value of the solar constant and its spectrum have been defined as a standard value called air mass zero (AM0) and takes a value of 1.366 kW/m2. The spectral irradiance is given in the Appendix.
- 1. , “Solar Energy Utilisation”, Khanna Publishers, 1980, p. 44.
- Log in or register to post comments
- 3 comment(s)
 Español
Español 한국어
한국어 简体中文
简体中文 Bahasa Indonesia
Bahasa Indonesia