Contact resistance losses occur at the interface between the silicon solar cell and the metal contact. To keep top contact losses low, the top N+ layer must be as heavily doped as possible. However, a high doping level creates other problems. If a high level of phosphorus is diffused into silicon, the excess phosphorus lies at the surface of the cell, creating a "dead layer," where light generated carriers have little chance of being collected. Many commercial cells have a poor "blue" response due to this "dead layer." Therefore, the region under the contacts should be heavily doped, while the doping of the emitter is controlled by the trade-offs between achieving a low saturation current in the emitter and maintaining a high emitter diffusion length.

Points of contact resistance losses at the interface between grid lines and semiconductor.
Contact resistance and Current Crowding
The finger metal has a much higher conductivity than the underlying doped semiconductor. Light generated current between the fingers travels laterally to the contacts and passes non-uniformly into the contacts with the highest concentration of current at the edge of the finger contact as shown below.
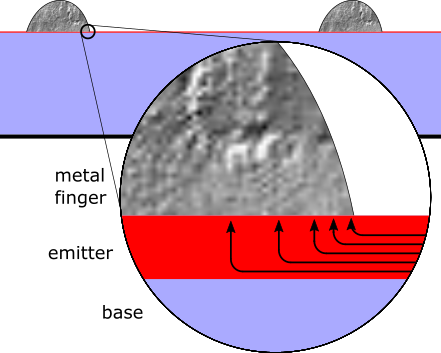
Current 'crowds' at the edge of the finger due to the lateral flow of current and the high conductivity of the metal finger compared to the doped emitter.
The transfer length characterizes the degree of current crowding. LT usually denotes the transfer length, but here we use transfer width, WT (in cm), so that it is not confused with the finger length.
$$W_{T}=\sqrt{\frac{\rho_{C}}{R_{\text {sheet}}}}$$
Where ρc is the contact resistance in Ωcm2, and Rsheet is the resistance of the emitter layer in Ω/□
Power Loss due to Contact Resistance
Current flows into each side of the finger so in determining the power loss we divide the finger in two.
The contact resistance in ohms at the finger is:
$$R_{c}=\left(W_{T} / L_f \right) R_{sheet} \operatorname{coth} \left( \frac{W_f } {2 W_T}\right)$$
For a very small transfer width (WT < Wf/2), the effective area for contact is equal to Lf × WT
$$R_c \simeq \frac{\rho_c}{L_f W_T}$$
For a transfer width greater than twice the finger width (WT > 2 Wf), there is no current crowding and the entire contact is available:
$$R_c \simeq \frac{2 \rho_c}{L_f W_f}$$
We divided the finger into two in the area above so there is only half the finger width available to each side.
The power loss at each side of the finger is I²RC:
$$P_{loss} = \frac {J_{MP}^2 S_f^2 L_f W_{T} R_{sheet} \operatorname{coth}\left( \frac{W_f } {2 W_T} \right)} {4}$$
To find the total loss of power due to contact resistance, multiply the previous equation by two times the number of fingers.
The fractional power loss is the power dissipated in the contact resistance divided by the power generated over the region I²RC/(VI).
$$ \begin{align} P_{loss.contact} & = \frac{I_{MP}^2R}{V_{MP}I_{MP}} \\& = \frac {J_{MP} S_f L_f R_c} {2 V_{MP}} \\ & = \frac {J_{MP} S_f W_{T} R_{sheet} \operatorname{coth}\left( \frac{W_f } {2 W_T} \right)} {2 V_{MP}}\end {align}$$
Where Ploss.contact is the fraction (0 to 1) power loss due to the contact resistance.
The contribution to series resistance in ohm cm² is:
$$R_{s.contact} = \frac { S_f W_{T} R_{sheet} \operatorname{coth}\left( \frac{W_f } {2 W_T} \right)} {2}$$
In commercial screen-printed solar cells, the contact resistance varies across the wafer. The physics of silver paste firing are quite complicated so small differences in surface topology and local heating cause large variations in the quality of the silver-silicon bond.
