Until the late 19th century most people used local solar time so that noon was when the sun was directly overhead, and each town had its own definition. Transport was slow, so it did not matter that the time in a town miles away varied by a few minutes. The advent of railways necessitated more accurate time keeping and time zones were introduced to keep an entire region on the same time1. Time zones follow political boundaries so that local time may be up to 2 hours different from solar time.
Local Solar Time (LST) and Local Time (LT)
Twelve noon local solar time (LST) is defined as when the sun is highest in the sky. Local time (LT) usually varies from LST because of the eccentricity of the Earth's orbit, and because of human adjustments such as time zones and daylight saving.
Local Standard Time Meridian (LSTM)
The Local Standard Time Meridian (LSTM) is a reference meridian used for a particular time zone and is similar to the Prime Meridian, which is used for Greenwich Mean Time. The LSTM is illustrated below.
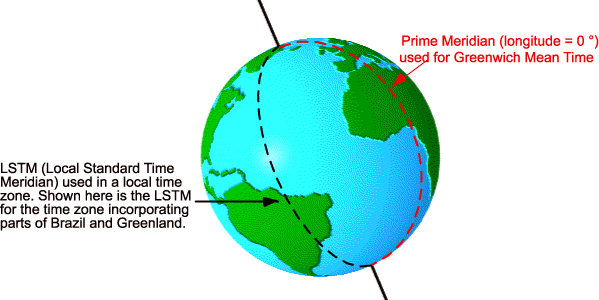
The (LSTM) is calculated according to the equation:
where ΔTUTC is the difference of the Local Time (LT) from Universal Coordinated Time (UTC) in hours. ΔTUTC is also equal to the time zone. 15°= 360°/24 hours. For instance, Sydney Australia is UTC +10 so the Local Standard Time Meridian is 150 °E. Phoenix, USA is UTC -7 so the LSTM is 105 °W
Equation of Time (EoT)
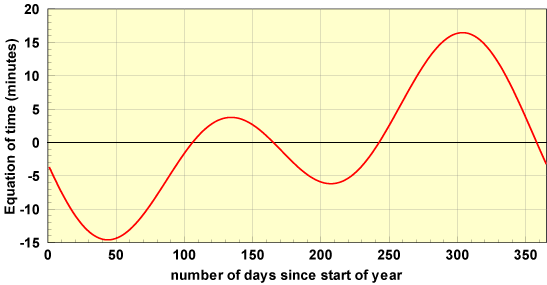
The equation of time (EoT) (in minutes) is an empirical equation that corrects for the eccentricity of the Earth's orbit and the Earth's axial tilt. An approximation 2 accurate to within ½ minute is:
where
$$B=\frac{360}{365}(d-81)$$
in degrees and d is the number of days since the start of the year. The time correction EoT is plotted in the figure below.
Time Correction Factor (TC)
The net Time Correction Factor (in minutes) accounts for the variation of the Local Solar Time (LST) within a given time zone due to the longitude variations within the time zone and also incorporates the EoT above.
$$T C=4(\text {Longitude}-LSTM)+EoT$$
The factor of 4 minutes comes from the fact that the Earth rotates 1° every 4 minutes.
Local Solar Time (LST)
The Local Solar Time (LST) can be found by using the previous two corrections to adjust the local time (LT).
$$LST=L T+\frac{T C}{60}$$
Hour Angle (HRA)
The Hour Angle converts the local solar time (LST) into the number of degrees which the sun moves across the sky. By definition, the Hour Angle is 0° at solar noon. Since the Earth rotates 15° per hour, each hour away from solar noon corresponds to an angular motion of the sun in the sky of 15°. In the morning the hour angle is negative, in the afternoon the hour angle is positive.
$$HRA=15^{\circ}(LST-12)$$
Local Time to Local Solar Time Calculator
The conversion of LT to LST is complicated by the world’s time zones and there is not a simple conversion from a location to its time zone. The calculator below uses Google to determine the time zone from its location. It will accept any description such as an address, city name, airport code and then show its location on a map. It also determines the most up to date time zone for that location. The most commonly used location is assumed so that simply “Paris” will be Paris, France whereas “Paris, Texas” will be Paris in the US state of Texas.
Enter a location above to get its longitude and time zone. Once the time zone is determined, the latitude is not needed when calculating the local solar time. The longitude and time zone can also be entered directly without having to use the lookup. Standard time is used and there is no correction for Daylight Savings.
- 1. , “The Standardization of Time: A Sociohistorical Perspective”, American Journal of Sociology, vol. 88, pp. 1-23, 1982.
- 2. , “Note on the Equation, of Time”, The Mathematical Gazette, vol. 10, no. 155, pp. 372 - 375, 1921.
- Log in or register to post comments
- 7 comment(s)
 Español
Español 한국어
한국어 简体中文
简体中文 Bahasa Indonesia
Bahasa Indonesia
