The power incident on a PV module depends not only on the power contained in the sunlight, but also on the angle between the module and the sun. When the absorbing surface and the sunlight are perpendicular to each other, the power density on the surface is equal to that of the sunlight (in other words, the power density will always be at its maximum when the PV module is perpendicular to the sun). However, as the angle between the sun and a fixed surface is continually changing, the power density on a fixed PV module is less than that of the incident sunlight.
The amount of solar radiation incident on a tilted module surface is the component of the incident solar radiation which is perpendicular to the module surface. The following figure shows how to calculate the radiation incident on a tilted surface (Smodule) given either the solar radiation measured on horizontal surface (Shoriz) or the solar radiation measured perpendicular to the sun (Sincident).
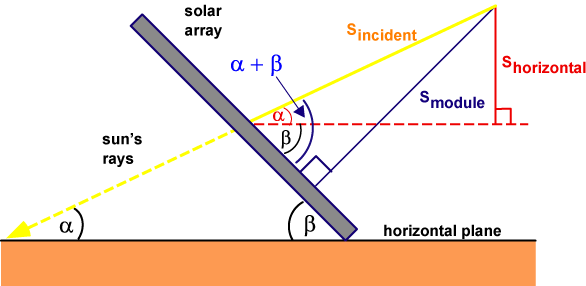
Tilting the module to the incoming light reduces the module output.
The equations relating Smodule, Shoriz and Sincident are:
$$S_{horizontal}=S_{incident} \sin \alpha$$
$$S_{module}=S_{incident} \sin (\alpha+\beta)$$
where
α is the elevation angle; and
β is the tilt angle of the module measured from the horizontal.
The elevation angle has been previously given as:
$$\alpha=90-\phi+\delta$$
where \(\phi\) is the latitude; and
\(\delta\)is the declination angle previously given as:
$$\delta=23.45^{\circ} \sin \left[\frac{360}{365}(284+d)\right]$$
where d is the day of the year. Note that from simple math (284+d) is equivalent to (d-81) which was used before. Two equations are used interchangeably in literature.
From these equations a relationship between Smodule and Shoriz can be determined as:
$$S_{module}=\frac{S_{Shorizontal} \sin (\alpha+\beta)}{\sin \alpha}$$
The following active equations show the calculation of the incident and horizontal solar radiation and that on the module. Enter only one of Smodule, Shoriz and Sincident and the program will calculate the others.
The tilt angle has a major impact on the solar radiation incident on a surface. For a fixed tilt angle, the maximum power over the course of a year is obtained when the tilt angle is equal to the latitude of the location. However, steeper tilt angles are optimized for large winter loads, while lower title angles use a greater fraction of light in the summer. The simulation below calculates the maximum number of solar insolation as a function of latitude and module angle.
The effect of latitude and module tilt on the solar radiation received throughout the year in W.h.m-2.day-1 without cloud. On the x-axis, day is the number of days since January 1. The Module Power is the solar radiation striking a tilted module. The module tilt angle is measured from the horizontal. The Incident Power is the solar radiation perpendicular to the sun's rays and is what would be received by a module that perfectly tracks the sun. Power on Horizontal is the solar radiation striking the ground and is what would be received for a module lying flat on the ground. These values should be regarded as maximum possible values at the particular location as they do not include the effects of cloud cover. The module is assumed to be facing south in the northern hemisphere and north in the southern hemisphere. For some angles, the light is incident from the rear of the module and in these cases the module power drops to 0.
As can be seen from the above animation, for a module tilt of 0°, the Module Power and Power on Horizontal are equal since the module is lying flat on the ground. At a module tilt of 80°, the module is almost vertical. The Module Power is less than the Incident Power except when the module is perpendicular to the sun's rays and the values are equal. The module is orientated to the equator so it faces north in the Southern Hemisphere and south in the Northern Hemisphere. As module moves from the Northern to Southern Hemisphere (latitude = 0°), the module is turned to face in the opposite direction and so the Module Power curve flips. When the light is incident from the rear of the module the Module Power drops to zero . Try setting the latitude to your location and then varying the module tilt to see the effect on the amount of power received throughout the year.
