Diode Equation

Overview

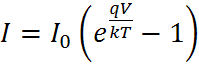
I₀ is directly related to recombination, and thus, inversely related to material quality.
Non-ideal diodes include an "n" term in the denominator of the exponent. N is the ideality factor, ranging from 1-2, that increases with decreasing current.

Ideal Diodes

The diode equation gives an expression for the current through a diode as a function of voltage. The Ideal Diode Law, expressed as:

Ideal diode equation

where:
I = the net current flowing through the diode;
I₀ = "dark saturation current", the diode leakage current density in the absence of light;
V = applied voltage across the terminals of the diode;
q = absolute value of electron charge;
k = Boltzmann's constant; and
T = absolute temperature (K).

The "dark saturation current" (I₀) is an extremely important parameter which differentiates one diode from another. I₀ is a measure of the recombination in a device. A diode with a larger recombination will have a larger I₀.

Note that:

I₀ increases as T increases; and
I₀ decreases as material quality increases.

At 300K, kT/q = 25.85 mV, the "thermal voltage".

Non-Ideal Diodes

For actual diodes, the expression becomes:

Diode equation

where:
n = ideality factor, a number between 1 and 2 which typically increases as the current decreases.

The diode equation is plotted on the interactive graph below. Change the saturation current and watch the changing of IV curve. Note that although you can simply vary the temperature and ideality factor the resulting IV curves are misleading. In the simulation it is implied that the input parameters are independent but they are not. In real devices, the saturation current is strongly dependent on the device temperature. Similarly, mechanisms that change the ideality factor also impact the saturation current. Temperature effects are discussed in more detail on the Effect of Temperature page.

The diode law is illustrated for silicon on the following picture. Increasing the temperature makes the diode to "turn ON" at lower voltages.

Effect of temperature

The diode law for silicon - current changes with voltage and temperature. For a given current, the curve shifts by approximately 2 mV/°C. The trend is opposite to the simulation due to the changing saturation current I₀