임의의 기울기와 방향을 가진 모듈의 경우 방정식은 아래와 같이 좀 더 복잡해진다.
Solar Intensity
α는 태양의 고도각, Θ는 태양의 방위각, 그리고 β는 모듈의 경사각이다. 바닥에 평행하게 놓인 모듈은 β=0°이고, 수직 모듈은 β=90°이다. Ψ는 모듈이 향하는 방위각이다. 거의 대부 분의 모듈은 적도를 향하도록 정렬된다. 남반구에서의 모듈은 Ψ = 0°에 북쪽을 향하게 되 고, 북반구에서의 모듈은 통상 Ψ = 180°로 정남을 향하게 된다. Smodule과Sincident은 각각 모 듈 위에서의 빛의 세기와 입사되는 빛의 세기로 단위는 W/m² 인데, Sincident은 직달 성분만 포함한다.
입사되는 태양광선이 모듈 면에 수직인, 태양을 똑바로 향하는 모듈의 기울기 각도는 태양 의 천정각(90-α=β)과 같고, 모듈의 방위각은 태양의 방위각과 같다(Ψ=Θ).
아래 계산식은 태양의 위치를 에어매스(AM, 대기질량지수) 공식과 연계한 것으로 임의의 기울기와 방향을 가진 모듈 위에서의 입사 태양광의 세기를 계산하는데 사용할 수 있다.
Light Intensity
태양의 방향을 계산하는데 벡터 사용하기 (Using Vectors to Calculate Solar Direction)
기울기와 방향의 개수가 더 복잡해지면 태양의 방위각과 고도각을 벡터로 변환하는 것이 더 편하다. 그 사례로 역시 임의의 기울기와 방향에 위치한 건물 위에 경사진 모듈이 설치된 경우를 들 수 있다. 벡터를 사용하는 것이 편하다는 것은 경사진 면에서의 빛의 세기가 감 소하는 것은 단순히 입사 광선과 모듈의 법선면 사이의 벡터적(dot product)이라는 사실에 근거한 것이다.
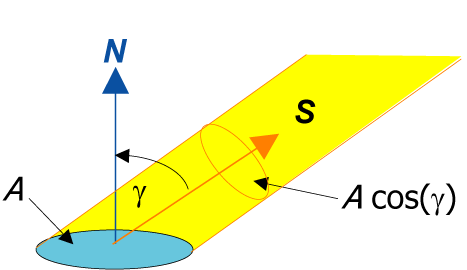
특정 각도로 표면에 부딪치는 빛은 더 넓은 면적으로 퍼져 나간다. 빛 세기의 감소는 단위 벡터 S와 N의 벡터적이다.
Solar Intensity Vector
여기서, Smodule과 Sincident은 앞에서 정의한 것과 같고, S는 태양을 향하는 단위 벡터 점이고, N은 모듈의 면에 법선인 단위 벡터이고, γ는 2 벡터들 사이의 각도이다.
